Visualisation Scientifique :

Algorithme

Programmation

Affichage d’une sphère par l’algorithme du Marching Cubes

Resultat obtenu

Algorithme

L’algorithme du Marching Cubes a été inventé par Bill LORENSEN et Harvey CLINE. Il s’agit d’une méthode surfacique permettant d’extraire une surface équipotentielle (isosurface) d’un maillage structuré et uniforme 3D. Le Marching Cubes est une extension 3D de la technique du Marching Squares 2D vu dans la partie précédente.

Le principe est de calculer, les différentes configurations que peut prendre l’isosurface dans un élément de volume, selon la répartition des intersections de l’isosurface sur les arrêtes de cet élément de volume.

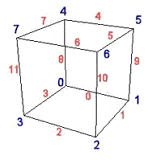
Pour uniformiser les expressions, le code et les calculs nous utiliserons la numérotation des sommets et arêtes suivantes :

Dans notre cas, l’élément de volume est un cube, nous avons donc 8 sommets, 12 arêtes et chaque sommet peut prendre 2 états.

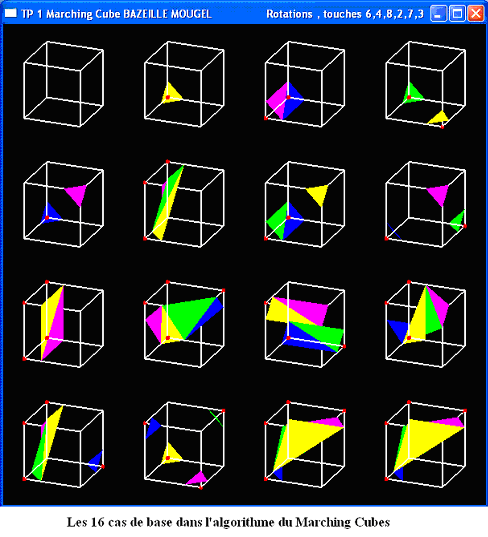
Cela donne donc 2^8 = 256 configurations possibles, qui sont autant de façon pour une surface d’intersecté les arêtes du volume. Chaque configuration correspond à un ensemble de facettes tracées à l’intérieur du volume, mais la présence de nombreux cas symétriques permet de se ramener à 16 configurations de base.

 

Chaque sommet en rouge indique que son isovaleur est inférieure à l’isosurface.

 

Up

Programmation

Les Structures utilisées :

• Point3D qui contient 3 entiers , les coordonnées dans l’espace d’un point.
• Grille qui représente un cube et contient 8 Point3D et leurs 8 poids associés.
• Triangle qui contient 3 Point3D.

Les fonctions utilisées :

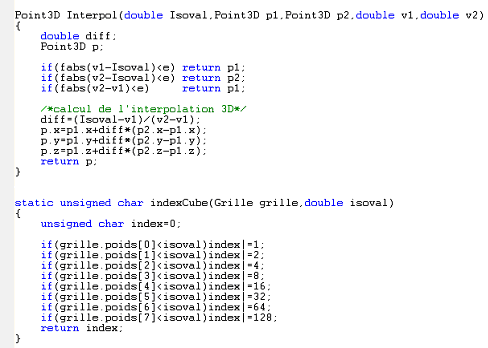
• Fonction Interpolation Linéaire ( Comme dans Marching Square mais en 3D )

• Fonction IndexCube

Cette fonction permet de générer un octet dont chaque bit représente l’état d’un des sommets du cube. Si la poids du sommet est supérieur a l’isovaleur le bit est a 1 sinon il est a 0.

Cet index cube est ensuite utilisé par la table des arêtes. TableDesAretes[IndexCube] indique le numéro des arêtes intersectées par l’isosurface.

Comme il y a 12 arêtes différentes dans un cube les données contenues dans la table des arêtes sont sur 12 bits soit 3 caractères en hexadécimal.

• Fonction Calcul Points d’intersection

Sachant le numéro des arêtes qui sont intersectées on peut maintenant calculer la liste des points d’intersection entre l’isosurface et le cube élémentaire examiné.
Cette fonction fait donc appel a Interpolation Linéaire et remplie un tableau contenu l’ensemble des points d’intersection.

• Fonction Draw Marching Cubes

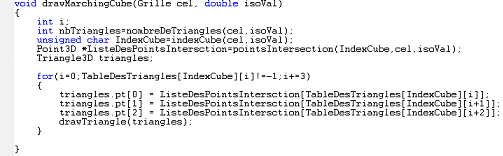
Cette fonction dessine l’ensemble des facettes sur le cube élémentaire examiné.
Elle fait appel a notre deuxième table vu précédemment appelé TableDesTriangles car cette contient des liste ordonnées des arêtes intersectées. Ces listes permettent de calculer les points d’intersection puis de générer des facettes triangulaires.

Egalement les fonctions

• DrawPoint qui dessine un point.
• InitPoids qui initialise les poids pour les 16 configurations de base du Marching cubes.
• InitCube pour l’initialisation des coordonnées d’un cube.
• DrawTriangle qui dessine une facette.
• DrawCube qui dessine un cube.
• Display fonction qui gère l’ensemble de l’affichage du programme.
• Clavier fonction qui gère l’ensemble des commandes clavier.
• Reshape fonction de redimensionnement de la fenêtre d’affichage.
• Et la fonction Main qui gère l’exécution du programme.

Up

Affichage d’une sphère par l’algorithme du Marching Cubes.

Nous disposons d’un maillage 3D uniforme comportant des informations. Chaque élément de volume du maillage est parcouru. Pour chacun de ces volumes, les poids des sommets du cube élémentaire sont comparés à l’isovaleur. En fonction des ces tests, un index binaire (8 bits=1 octet) est créé (bit à 1 si la valeur du sommet est inférieure à l’isovaleur, 0 sinon).
A partir de cet index, on consulte la table qui indique l’état topologique de l’élément de volume (quelles arrêtes sont intersectées).
Pour chaque arête intersectée, on calcule par interpolation linéaire, les coordonnées du point d’intersections et ensuite il suffit de dessiner ou de stocker la facette.
L’ensemble du volume que l’on veut représenter est découpé en un nombre important de facettes.
En résumé :
Pour chaque volume du maillage :

• Créer un index (8 bits) contenant l’état de chaque sommet.
• Trouver les arrêtes intersectées et calculer les coordonnées d’intersection.
• Dessiner les facettes.

Up

Resultat obtenu

L’équation de sphère est un bon moyen de mettre en valeur l’influence de l’isovaleur de référence car l’isosurface affiché correspond à une sphère qui pour rayon l’isovaleur de référence (comme si toutes les sphères étaient imbriquées les unes dans les autres).
Elle permet aussi de voir nettement l’influence de la taille du cube élémentaire.

L’équation de la sphère est la suivante : x² + y² + z² = r²

On utilise dans ce programme des fichiers Lumière et Calcul de Normal pour un meilleur rendu d’affichage.
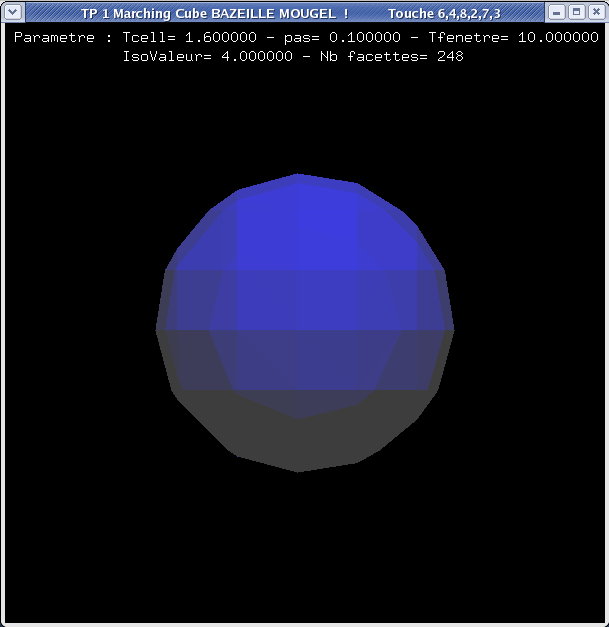
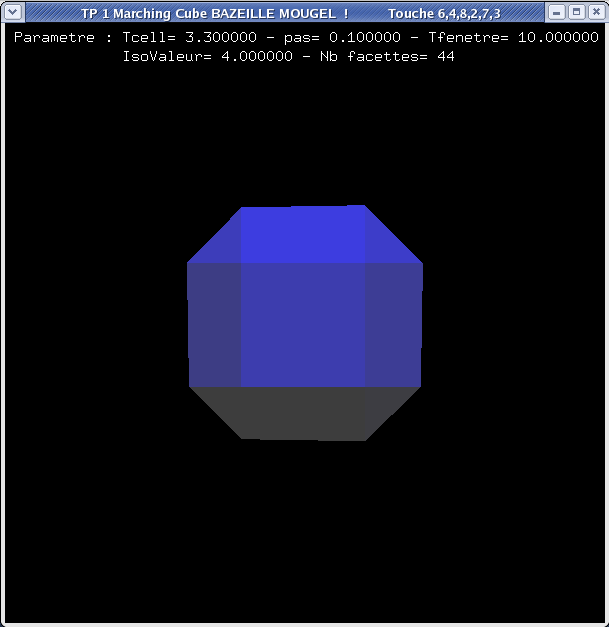
Ci dessous 3 exemples d’une sphère par le Marching Cubes avec :

1. Taille de cellule élémentaire 3.3 , sur taille fenêtre de 10 > 44 facettes.
2. Taille de cellule élémentaire 1.6 , sur taille fenêtre de 10 > 248 facettes.
3. Taille de cellule élémentaire 0.3 , sur taille fenêtre de 10 > 6632 facettes.

Nombre de facette : 6632 Taille de la cellule: 0.3 IsoValeur : 4	Nombre de facette : 248 Taille de la cellule: 1.6 IsoValeur : 4	Nombre de facette : 44 Taille de la cellule: 3.3 IsoValeur : 4

Up

Réalisé par : Stéphane Bazeille & Baptiste Mougel

Enseignant : Michel EBOUEYA Maitre de Conférences